Statistical Test of Cluster Memberships

Introduction

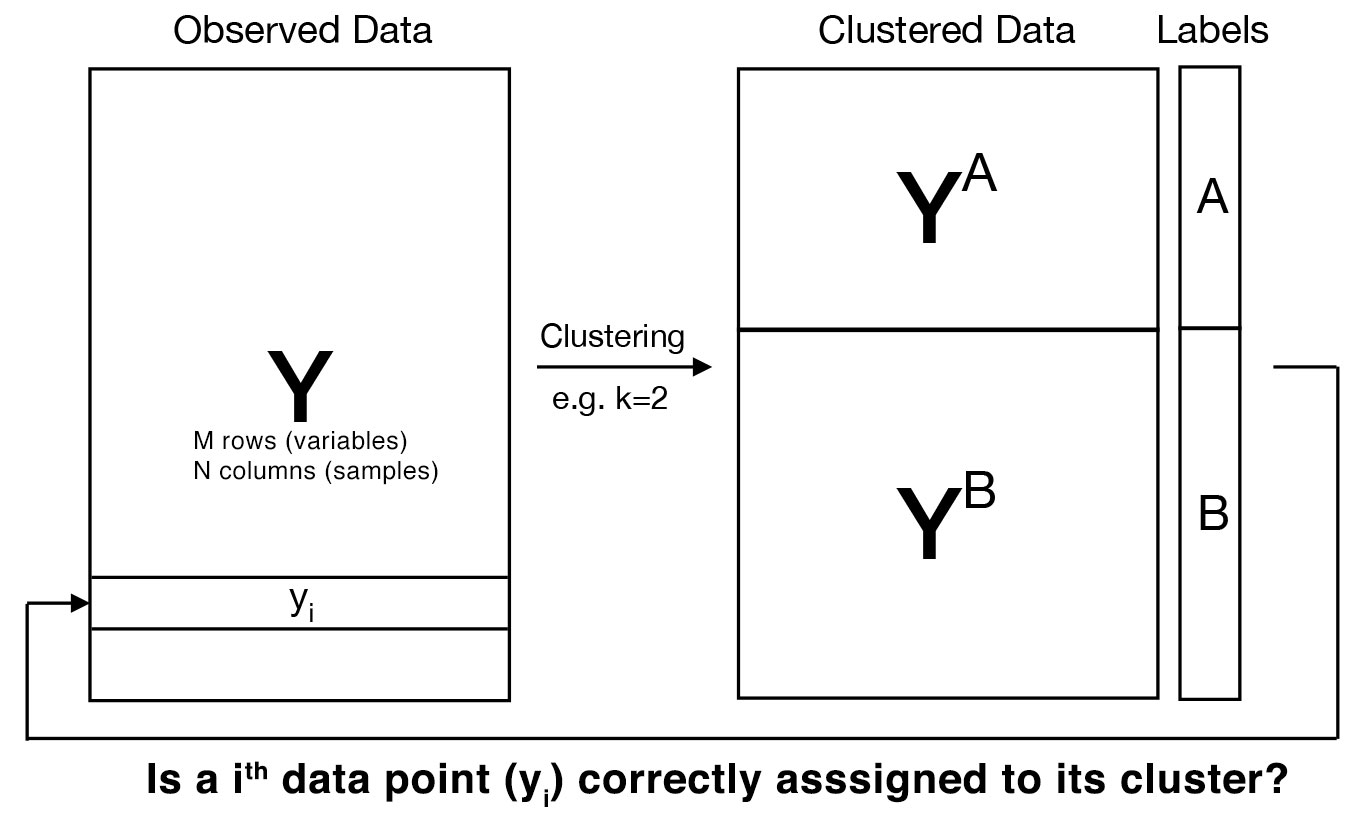
Clustering algorithms can classify data points in an unsupervised manner. Specifically, clustering can provide how to divide M data points (of N dimensions) into K clusters. Most of popular clustering algorithms are so-called “hard clustering”, meaning that each of M data points is univocally assigned to one of K clusters. This establishes cluster memberships of M data points across K clusters. Then, how can we evaluate cluster membership of M data points?

Example of mtcars

For example, let’s consider a mtcars dataset of M=32 cars and their characteristics from 1974 Motor Trend US magazine. By applying clustering to M=32 cars, we can obtain groups of cars that exhibit similar characteristics. Let’s imagine how M=32 cars are classified into K=2 clusters using K-means clustering. After clustering is done, our goal is then to evaluate (e.g., calculate statistical significance) how well these cars have been placed into 2 different cluters.

Jackstraw test for cluster membership

In a large and noisy dataset, some data points may have been incorrectly clustered or contains no significant signals. The jackstraw test for cluster membership helps evaluate whether data points are correctly assigned to their given clusters.

We are conducting hypothesis testing of association between a cluster center and an individual data point (of N dimensions)². This provides p-values and posterior inclusion probabilities (PIPs), which you can use to identify data points that are reliably associated with that cluster.

R code

Let’s look at how to do this, using the R package jackstraw. The key function is jackstraw_kmeans calculating the jackstraw p-values when applying K-means clustering. Also, jackstraw_pam and jackstraw_MiniBatchKmeans are for Partitioning Around Medoids (PAM) and Mini Batch K-means clustering. A generic algorithm which you may use other clustering algorithms is available on jackstraw_cluster.

We process mtcars (a built-in dataset in R) for clustering. Remove 2 binary columns and normalize each column³.:

# see the summary of mtcars dataset
head(mtcars)

##                    mpg cyl disp  hp drat    wt  qsec vs am gear carb
## Mazda RX4         21.0   6  160 110 3.90 2.620 16.46  0  1    4    4
## Mazda RX4 Wag     21.0   6  160 110 3.90 2.875 17.02  0  1    4    4
## Datsun 710        22.8   4  108  93 3.85 2.320 18.61  1  1    4    1
## Hornet 4 Drive    21.4   6  258 110 3.08 3.215 19.44  1  0    3    1
## Hornet Sportabout 18.7   8  360 175 3.15 3.440 17.02  0  0    3    2
## Valiant           18.1   6  225 105 2.76 3.460 20.22  1  0    3    1

# remove two binary columns
car <- as.matrix(mtcars[,-c(8,9)])
zcar <- apply(car, 2, function(x) (x-mean(x))/sd(x))

In this example, another R package anocva is used determine the number of clusters. However, this completely depends on your data, applications, and analysis goals. Please carry out careful exploratory data analysis.:

# install.packages("anocva")
library(anocva)
myKmeans = function(dist, k){
  return(kmeans(dist, k, iter.max = 100, nstart = 10)$cluster)
  }
distMatrix = as.matrix(dist(zcar))
distMatrix = checkRange01(distMatrix)
nClust(distMatrix, p = 1, maxClust = 10, myKmeans)

## [1] 2

We apply K-means clustering to the normalized mtcars dataset. The function kmeans cluster 32 cars in this dataset. The jackstraw test for cluster membership with B=1000 iteration is applied. We choose s=3, approximately 10% of the cars:

# set a rng seed for reproducibility
set.seed(1)
# apply k-means clustering
kmeans.car = kmeans(zcar, centers=2, nstart = 10, iter.max = 100)

library(jackstraw)
# apply k-means clustering
jackstraw.out <- jackstraw_kmeans(dat=zcar,
                                  kmeans.dat=kmeans.car,
                                  s=3,
                                  B=1000,
                                  nstart = 10,
                                  iter.max = 100)
jackstraw.out$pip <- pip(jackstraw.out$p.F)

Here are a few histograms to look at. For example, one may look at observed and null F-statistics for diagnostic reasons. We could use PIPs to filter or select some cars that are not good fits for that clusters.:

library(ggplot2)
library(tibble)
ggplot(as_tibble(jackstraw.out$p.F),aes(value)) +
  geom_histogram(binwidth=.1,center = .05) +
  labs(title = "P-values of cluster memberships")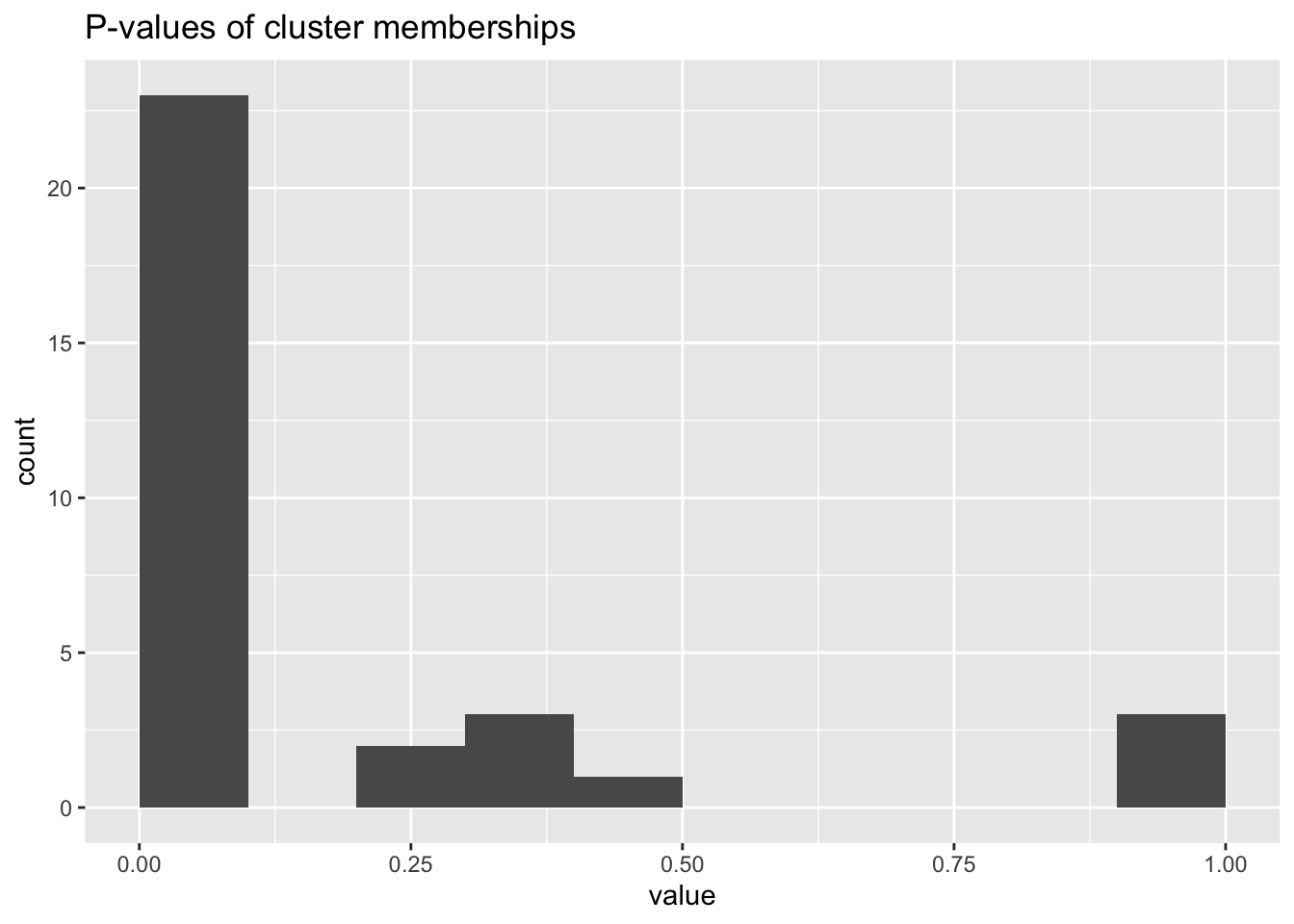

ggplot(as_tibble(jackstraw.out$pip),aes(value)) +
  geom_histogram(binwidth=.1,center = .05) +
  labs(title = "Posterior inclusion probabilities")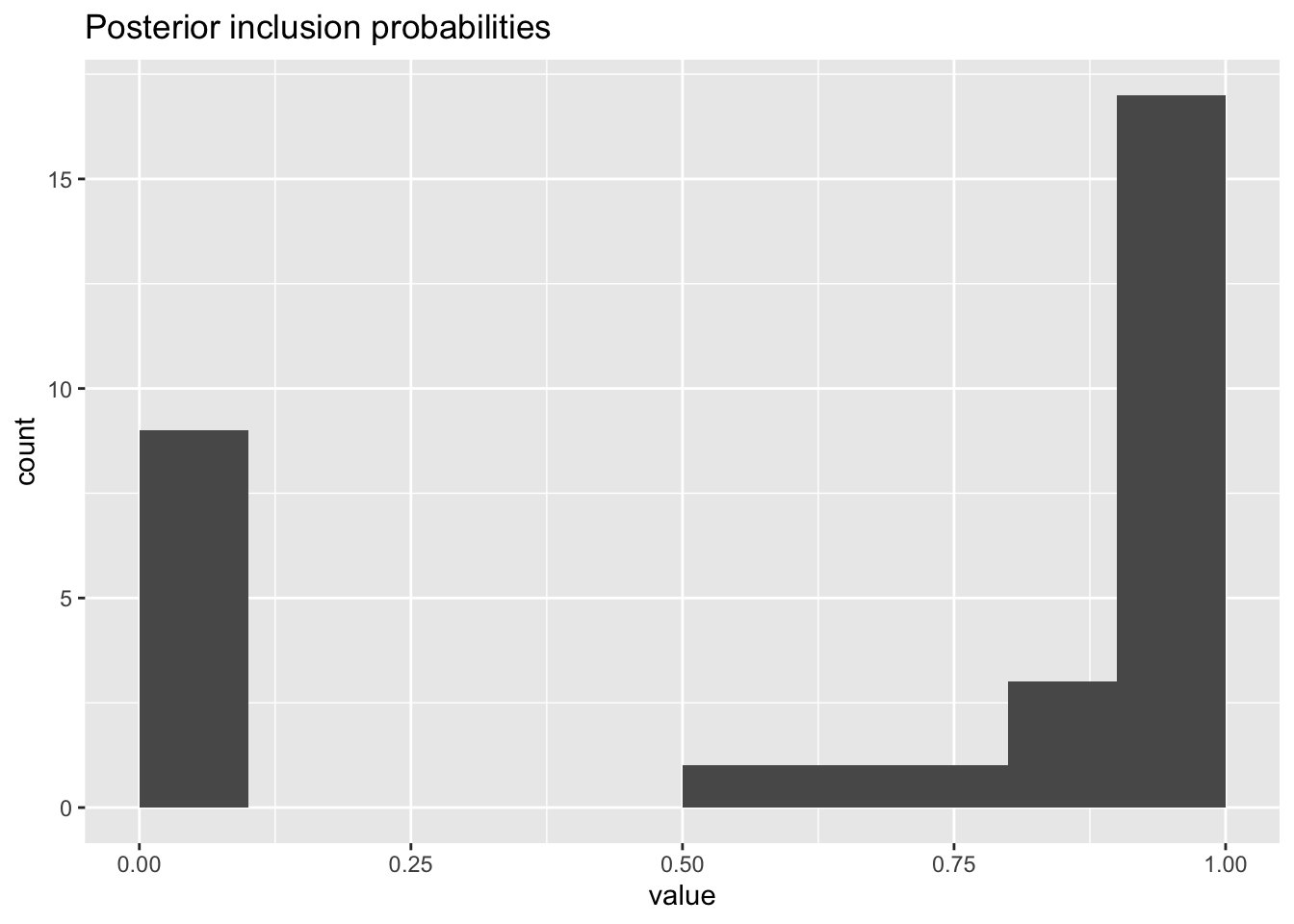

ggplot(as_tibble(jackstraw.out$F.obs),aes(value)) +
  geom_histogram(binwidth=20,center = 10) +
  labs(title = "Observed F-statistics")

The jackstraw algorithm

An empirical distribution of association statistics under the null hypothesis must account for the fact that clustering depends on observed data. If clusters or cluster centers are used directly against the observed data (from which these clusters are derived from), it’s called circular analysis, resulting in spurious associations and artificially inflated significances.

The jackstraw randomly chooses S data points (or rows in our example), where S is much smaller than N (N >> S). Each of S data points is resampled with replacement, resulting in S synthetic data points. The jackstraw data is a hybrid dataset consisted of N-S observed data points and S synthetic null data points. Then, the same clustering algorithm is applied on the jackstraw data, where association statistics between the cluster centers and S synthetic nulls are calculated. By repeating this resampling strategy B times, we obtain B * s null statistics, that forms an empirical distribution.

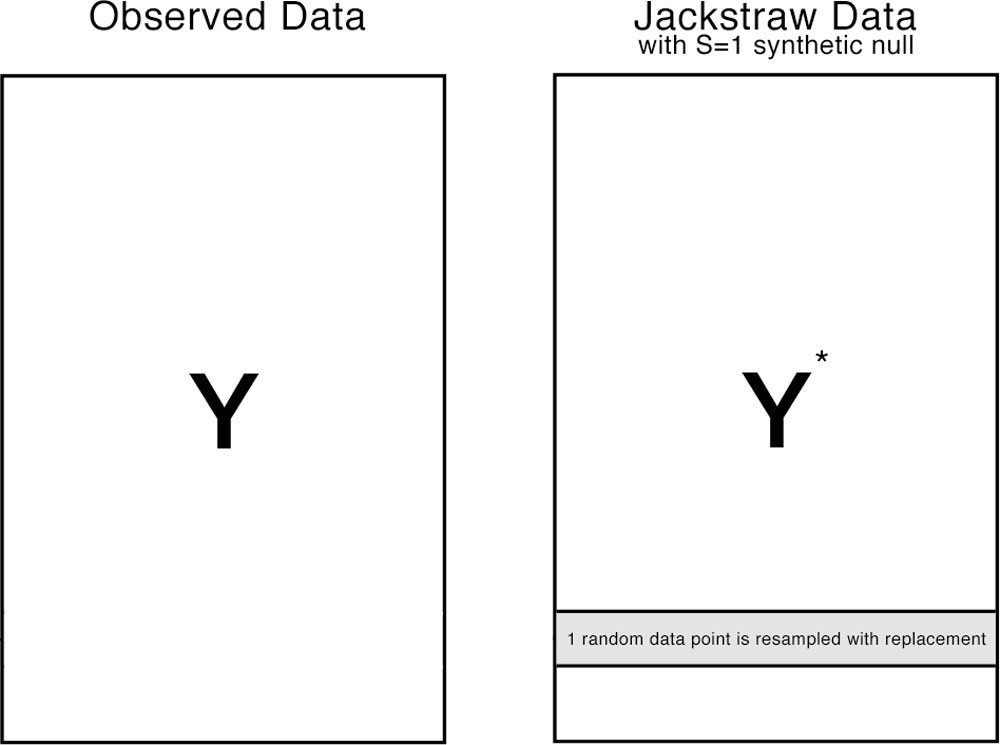
How is this different from bootstraping?

Bootstrapping or other resampling plans create a completely null dataset, in which no cluster structure exists. In contrast, we want to preserve the overall cluster structure, such that K clusters still exist in the jackstraw data and their cluster centers are asymptotically identical to their original centers. Since those synthetic nulls do not belong to any cluster, we can use them to establish a empirical distribution of null association statistics.

Cluster stability and related challenges

There has been important research focusing on cluster stability, asking two related questions:

• are these clusters stable/reliable?
• how many clusters exist in this data?

This leads to statistical measures⁴ as K would be varied (e.g., from 2 to a large number), allowing us to choose an optimal value for K. Generally speaking, instead of examining cluster structure or stability, the jackstraw focuses on reliability of individual data points. The jackstraw requires K to be specified.

P-value troubleshooting

Always, examine the histogram of p-values. Behaviors of p-values are important, and even allow us to diagnose the problems with data, algorithms, or hyperparameters. Please see a blog post by David Robinson on how to interpret a p-value histogram⁵.

Posterior inclusion probabilities (PIPs) are empirical Bayesian measures, that are calculated from the set of p-values. It’s simply 1 - lfdr (local false discovery rate). For an introduction, see a blog post by Michael Love on Intuition behind local FDR⁶. There are several ways⁷ to estimate lfdr. By default, we use the qvalue package.

You may get into an error due to unability to estimate a proportion of null hypotheses, pi0⁸. Underneath, qvalue::pi0est is used and in some cases, an optional argument lambda may help. Also, try to set pi0=1 manually or estimate pi0 in some other ways.